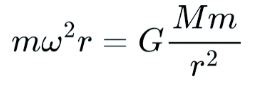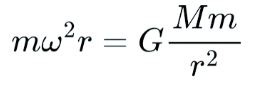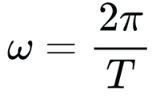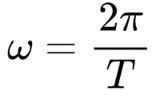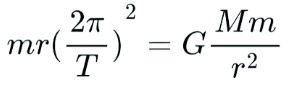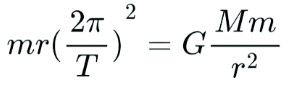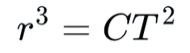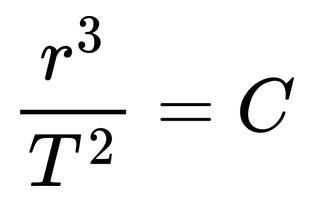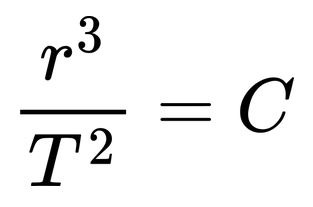Music of the Spheres

Awhile back, a fellow podcaster named Karaleigh Garrison made a comment about how she had edited some background music for her podcast, and she'd removed something called the music of the Sun rising or something similar to that.

And at first I thought yeah, that is kind of weird—the music of the Sun. But then I remembered that there is this theory of music of the spheres. I'd heard about it a long time ago, but I haven't really thought much of it until now.

Let’s take a look at this fascinating theory that has its roots in ancient Greece.

Pythagoras & Celestial Harmony

The music of the spheres is also known as Musica Universalis or Harmony of the Spheres, and dates back to the time of Pythagoras, around 600 to 500 BC. Known for his mathematical prowess (you’ve heard of the Pythagorean Theorem?), Pythagoras was also deeply involved in the study of music. He was the one who originated this idea and he believed that the celestial spheres--the planets, the stars, anything up in the sky--produced a vibration that, while you would not be able to hear it with your ears, it must sound musical and they would all be working together in a harmony.

Pythagoras was the first to discover that music is mathematical and that there's a relationship between music and numbers. He believed very strongly in the significance of numerology; that numbers exist outside of the human mind and that they govern the existence of life in the universe.

Mathematics of Music

Pythagoras was the first to study music mathematically. He would measure the lengths of strings and quantify their relationship between the sound when they vibrated the length of the string. That is, the ratio of the sound to the length of the string.

He discovered that the most harmonious musical intervals are the octave, the 5th and the 4th. Pythagoras discovered these relationships and there's a concept called Pythagorean tuning where you tune the frequency based on the ratio of 3 to 2, which is known as the pure perfect fifth. This is the easiest frequency to tune by ear.

Pythagoras believed that the essence of all things is numbers and that the universe is sustained by harmony. He and his followers often used music for health. They believed that medicine was to be used for the purification of the body, and music was for the purification of the soul.

Disagreements

Now one of Pythagoras’ contemporaries, Aristotle, rejected this idea of the music of the spheres because he believed that if the planets and stars made a sound, it would be so great that it would place a huge actual physical force on the human body on Earth.

Since we just don't feel that, Atristotle didn't believe that it was actually happening. He agreed with the theory that it could happen, but that it wasn’t physically happening.

The celestial music is something that could not be heard, because we don't feel a physical effect.

Johannes Kepler & Musica Universalis

The first known use of the term Musica Universalis was in 1609 by Johannes Kepler.

If you're into astronomy, you’ve heard of this very famous astronomer, and likely know his third law of orbital dynamics, which we'll get to in a second.

In this, he details his theory that the motion of the six known planets could be described by musical intervals and harmonies. Now, he knew that these harmonies could not be heard by the ear, but he did believe that they could be heard by the soul--that they affect humans on a soul level. Again, it's a philosophical concept rather than a physical one.

Kepler believed that these were very real effects that could be felt. He postulated that the orbits of the planets and their distances from the Sun are defined by the five Platonic solids. He found that the orbital motion he discovered almost perfectly matches musical harmonies.

Kepler is famous for developing three laws of orbital mechanics. The third law is the one that's most interesting here. Starting with Newton's law of gravitation, we set centripetal force equal to gravitational force (since gravity is what provides the centripetal force):

Replace angular momentum w with an expression using orbital period T:

Or,

Let's rearrange this so that r is on the right and T is on the left. We'll also gather all of the constants (m, M, G, and 2-pi) and call it C. What we'll have is:

Or, written as a ratio:

Here we see the ratio Pythagoras said was the perfect fifth—3:2.

When Kepler discovered this, it was confirmation to him that the planets indeed have music if they all have this ratio, this 3:2 ratio, which is a perfect harmony.

He also noted that when you take the ratio of the maximum and minimum orbital speeds, these ratios are almost perfectly equal to a constant musical interval such as octaves and fifths.

First, we have the ratio of the radius to the period, then we have the ratios of maximum and minimum speeds. Kepler found that all of these celestial ratios mimic musical ratios. He also liked to take these planetary motion equations and liken them to musical concepts. He compared the extreme speeds of planets (maxima and minima) with the idea of monophonic or polyphonic music.

If you have very high speed, you would have a single note. It would just sound like a very high pitch. The changing speeds along an orbit would be like having multiple singers or multiple instruments in a band. Based on the ratios of the maximum speeds, Kepler likened the solar system to a musical arrangement where he postulated Saturn and Jupiter would be bass, Mars would be a tenor, Venus and Earth would be altos, and Mercury would be a soprano.

Who knew our solar system was a perfect musical arrangement?